Given:
95% confidence level
sample size (n) = 91
Find: the lower and upper critical values in a chi-square distribution
Solution:
1. Calculate the degrees of freedom. Since the number of rows and columns is not specified in the question, we will subtract 1 from the sample size.
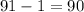
Our degrees of freedom (df) = 90.
2. Since this is two-tailed, subtract 0.95 from 1, then divide the result by 2.
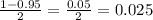
3. Let's now look at the chi-square distribution table and look for df = 90 with a probability of 0.025 on both the left and right tails.
Based on the table, the lower critical value is 65.647 while the upper critical value is 118.136.
Hence, the answer is Option B.