Question

I really need help is there any one that can help me rn ?

Answer 1

Given:

a function f(x) = (x-2)^2 is given.

Find:

we have to find the function whose graph is a result of horizonal shift of 2 units of the original graph.

Step-by-step explanation:

Since the given graph of the function is shifted 2 units horizontally,

and we know y is vertical axis, x is horizontal axis.

So put x = x+2 in the given function, we get

`\begin{gathered} f(x)=(x+2-2)^2 \\ f(x)=x^2 \end{gathered}`

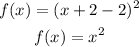
Therefore the graph of f(x)=(x-2)^2 is a result of horizontal shift of 2 units of f(x) = x^2.

The graphs are given for the reference