Question

27. A 4.00-g bullet is fired from a 4.50-kg gun with a muzzle velocity of 625 m/s. What is the speed of the recoil of the gun?

Answer 1

`-0.56m\/s`

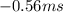
Step-by-step explanation

To find the recoil velocity of the gun, we have to apply the principle of conservation of momentum:

`mu+MU=mv+MV`

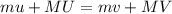
Since the total momentum of the system (gun and bullet) is conserved and 0 before the bullet is fired, the equation changes as follows:

`0=mv+MV`

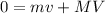
where m = mass of bullet = 4 g = 0.004 kg

M = mass of gun = 4.50 kg

v = velocity of bullet = 625 m/s

V = velocity of gun (recoil velocity)

Therefore, substituting the given values into the equation and solving for V:

`\begin{gathered} 0=(0.004\cdot625)+(4.5\cdot V) \\ \Rightarrow-4.5V=2.5 \\ \Rightarrow V=(2.5)/(-4.5) \\ V=-0.56m\/s \end{gathered}`

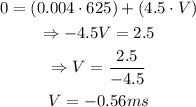
The negative