To calculate the first 5 terms of this sequence, we must start at the first, which is given, and use the equation to right the next one, and reaply the the next until we get to the fifth. k is the term which we are using. So, to calculate the second, we use k = 1:
So:
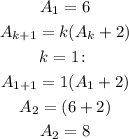
Now that we got A_2, we can use k=2 to calculate A_3:
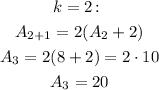
And so on, for k=3 and k=4:
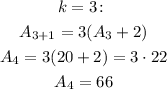
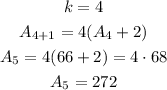
So, the five first terms are: 6, 8, 20, 66, 272.