start by ubicating the points in the cartesian plane
To identify if the points given is a rhombus the slope for the opposite sides must be equal in order for the sides to be parallel
Also the diagonals of the figure must be perpendicular between them.
FIND SLOPES FOR PS AND QR

apply for both sides
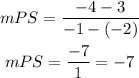
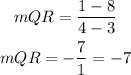
since both both sides have the same slope they are parallel.
FIND SLOPES FOR RS AND PQ

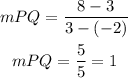
since both both sides have the same slope they are parallel.
FIND SLOPES FOR DIAGONAS QS AND PR
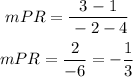
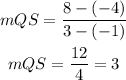
Find the product between the slopes
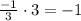
since the product of the slopes is -1, lines are perpendicular
Parallelogram PQRS is rhombus.