Let x be the number of liters of the 20% acid solution, and y be the number of liters of the 50% solution, then we can set the following system of equations:
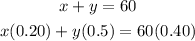
Solving the first equation for x and substituting it in the second equation we get:
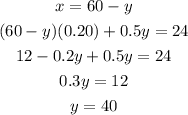
Therefore x=60-40=20.
Answer: Gave must add 20 liters of the 20% solution and 40 liters of the 50% solution.