As given by the question
There are given that the graph of a system of equation.
Now,
Solve every system of the equation which is given in options for the intersect value i.e. (1, 3).
And,
Then, the value of x = 1 and y = 3, will be the correct option because according to the graph, the intersection point is (1, 3).
Now,
we can directly solve option B for the intersection value.
So,
From the system of the equation of option B;
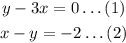
Now,
From the equation (1):

Put the value of y into the equation (2):
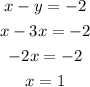
Then,
Put the value of x into equation (3) to find the value of y.
So,
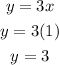
The value of x is 1 and the value of y is 3, which means the intersect value is (1, 3).
Hence, the correct option is B.