Question

A system of equations is made up of an ellipse and a hyperbola.

Answer 1

Ok, so

We want to find the equation of an ellipse centered at the origin with a horizontal major axis of 8 units and a minor axis of 6 units.

For this, let's remember the form of the equation of an ellipse:

`((x-h)^2)/(a^2)+((y-k)^2)/(b^2)=1`

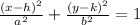
Where the center of the ellipse is located at the point (h,k).

If the ellipse is centered at the origin, then, h=0 and k=0, so the form of our equation will be:

`(x^2)/(a^2)+(y^2)/(b^2)=1`

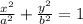
Now, we're given that our ellipse has a horizontal major axis of 8 units and a minor axis of 6 units. Since the major and minor axis are given by the parameters 2a and 2b, then, a=4 and b=3. the greater number will divide the x² term and a>b.

So, the equation of this ellipse is:

`(x^2)/(16)+(y^2)/(9)=1`

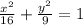
The graph of this ellipse will be something like: