Question

3. When looking through your telescope you discover a planet whose mean distancefrom the sun is 48.125 astronomical units. Use the results in Exercise 2 to find theperiod of this planet in days. (The period of Earth is 365.25 days.)4. Find the ratio of Pluto's mean distance from the sun to Mercury's mean distance.5. You are drawing a diagram of our solar system in which Mercury's mean distancefrom the sun is represented by 1 inch. How many inches will be needed to representPluto's mean distance from the sun?6. Redo the table given in Exercise 2 using scientific notation.

Answer 1

p = 121,938.7125 days

Here, we are given the value of k as approximately 1

We have a planet which has a mean distance of 48.125 astronomical units, we now need to get the period of this planet

From the Kepler's equation, the relation between k, p and a is given as

`k\text{ = }(p^2)/(a^3)`

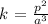
Since from calculations, k is 1, then we can rewrite the equation as;

`a^3=p^2`

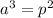
Now from the question, we have a as 48.125 astronomical units and p as what we want to find

Making substitutions, we have;

`\begin{gathered} (48.125)^3=p^2 \\ \\ p^2\text{ = 111,458.251953125} \\ \\ p\text{ = }\sqrt[]{\text{111,458.251953125}} \\ \\ p\text{ = 333.85} \end{gathered}`

Since 1 year is 365.25 days , then 333.85 years will be;

333.85 * 365.25 = 121,938.7125 days