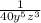Question

Simplify with positive exponents: $$\left(\frac{\left(-5y^3z^4\right)^2\left(yz^5\right)^{-2}}{\left(10y^4z\right)^3\left(y^3z^2\right)^{-1}}\right)$$

Answer 1

We have the expression:

`\mleft((\left(-5y^3z^4\right)^2\left(yz^5\right)^(-2))/(\left(10y^4z\right)^3\left(y^3z^2\right)^(-1))\mright)`

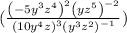
And we have to simplify it.

To do that, it is useful to see how many variables are in the expression and how they are placed. In this case, there are 2 variables (y and z) that are factors with different exponents and are within parenthesis that have their own exponents.

Then, we start by rearranging the factors and applying the exponents so there are no more parenthesis.

After that we will group each variable and simplify the exponents.

The steps to do this are:

`\begin{gathered} \mleft((\left(-5y^3z^4\right)^2\left(yz^5\right)^(-2))/(\left(10y^4z\right)^3\left(y^3z^2\right)^(-1))\mright) \\ ((-5)^2\cdot y^(3\cdot2)\cdot z^(4\cdot2)\cdot y^(-2)\cdot z^(5\cdot(-2)))/(10^3\cdot y^(4\cdot3)\cdot z^3\cdot y^(3\cdot(-1))\cdot z^(2\cdot(-1))) \\ (25\cdot y^6\cdot z^8\cdot y^(-2)\cdot z^(-10))/(1000\cdot y^(12)\cdot z^3\cdot y^(-3)\cdot z^(-2)) \end{gathered}`

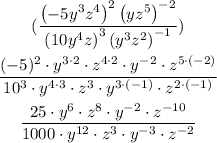
We can now group the similar variables as:

`\begin{gathered} ((25)/(1000))\cdot((y^6\cdot y^(-2))/(y^(12)\cdot y^(-3)))\cdot((z^8\cdot z^(-10))/(z^3\cdot z^(-2))) \\ (1)/(40)\cdot y^(6+(-2)-12-(-3))\cdot z^(8+(-10)-3-(-2)) \\ (1)/(40)\cdot y^(-5)\cdot z^(-3) \\ (1)/(40y^5z^3) \end{gathered}`

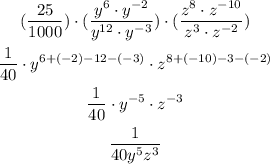
In this last part, we apply the product of a power rule, where we have a product of numbers with the same base. If that is the case, we can add the exponents:

`x^b\cdot x^c=x^(b+c)`

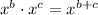
In the case of a quotient, we can apply the rule but the exponent in the denominator is substracted instead of added.

Answer:

The simplified expression is: 1/(40y^5z^3).

`(1)/(40y^5z^3)`