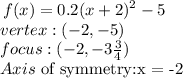Question

Help please !!! i’m trying to graduateplease refer left box as “box a” and the right as “box b” :)

Answer 1

Given:

There are given the two-equation:

`\begin{gathered} f(x)=-0.3(x-2)^2+5...(1) \\ f(x)=0.2(x+2)^2-5...(2) \end{gathered}`

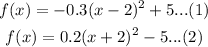
Step-by-step explanation:

According to the question, we need to find the values of vertex, the axis of symmetry, and focus.

Now,

First, find all values for the first equation:

So,

From the equation (1):

`\begin{equation*} f(x)=-0.3(x-2)^2+5 \end{equation*}`

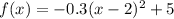
Then,

From the standard form of the equation of parabola:

`y=a(x-h)^2+k`

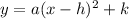
Where,

`\begin{gathered} vertex:(h,k) \\ Axis\text{ of symmetry:x=h} \end{gathered}`

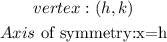
Now,

The values for the equation (1) are:

`\begin{gathered} vertex:(2,5) \\ Axis\text{ of symmetry: x=2} \\ focus:(2,4.166) \end{gathered}`

Now,

For the equation (2):

`\begin{equation*} f(x)=0.2(x+2)^2-5 \end{equation*}`

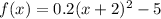
Then,

`\begin{gathered} vertex:(-2,-5) \\ focus:(-2,-3.75) \\ Axis\text{ of symmetry: x=-2} \end{gathered}`

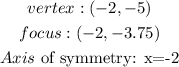
Final answer:

Hence, the all values for both box are shown below:

So,

For the first box:

`\begin{gathered} \begin{equation*} f(x)=-0.3(x-2)^2+5 \end{equation*} \\ vertex:(2,5) \\ focus:(2,4(1)/(6)) \\ Ax\imaginaryI s\text{ofsymmetry: x=2} \end{gathered}`

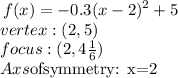
And,

For the second box:

`\begin{gathered} \begin{equation*} f(x)=0.2(x+2)^2-5 \end{equation*} \\ vertex:(-2,-5) \\ focus:(-2,-3(3)/(4)) \\ Axis\text{ of symmetry:x = -2} \end{gathered}`