Given that
The function is
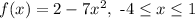
Explanation -
We have to find the maximum and minimum values of the function at the corresponding value of x.
Then,
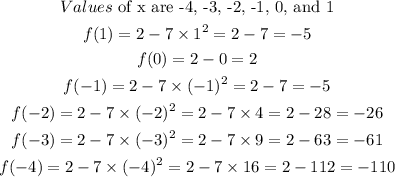
Hence, the maximum value of f(x) is 2 at x = 0
and minimum value of f(x) is -110 at x = -4
Final answer -
The final answer is the maximum value of f(x) is 2 at x = 0and minimum value of f(x) is -110 at x = -4