Question

Two ships left a port at the same time. One travelled due north and the other due east at average speeds of 25.5 km/h and 20.8 km/h, respectively. Find their distance apart

Answer 1

We will calculate the distance between the two ships as a function of time.

We can make a diagram for the situation as:

The ships are moving orthogonally, so we can calculate the distance as the hypotenuse of a right triangle.

The legs of this triangle will be the distance travelled.

As we know the speed v we can express the distance as the speed times the time: d = v*t.

We then can express the distance as:

`\begin{gathered} d=√(d_1^2+d_2^2) \\ d=√((v_1\cdot t)^2+(v_2\cdot t)^2) \\ d=√((20.8t)^2+(25.5t)^2) \\ d=√(20.8^2+25.5^2)\cdot t \\ d=√(432.64+650.25)\cdot t \\ d=√(1082.89)\cdot t \\ d\approx32.9t \end{gathered}`

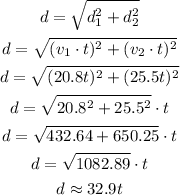
Answer: the distance is approximately 32.9t (in km), given that time is expressed in hours.