Question

The Washington, DC, region has one of the fastest-growing foreclosure rates in the nation, as 15,613 homes went into foreclosure during the one-year period ending in February 2008 (The Washington Post, June 19, 2008). Over the past year, the number of foreclosures per 10,000 homes is 131 for the Washington area, while it is 87 nationally. In other words, the foreclosure rate is 1.31% for the Washington, DC area and 0.87% for the nation. Assume that the foreclosure rates remain stable.

Required:
a. What is the probability that in a given year, fewer than 2 out of 100 houses in the Washington, DC area will go up for foreclosure?
b. What is the probability that in a given year, fewer than 2 out of 100 houses in the nation will go up for foreclosure?
c. Comment on the above findings.

Answer 1

The probability of fewer than 2 out of 100 houses going into foreclosure in the Washington, DC area and the nation can be found using the binomial probability formula. The findings suggest a higher foreclosure rate in the Washington, DC area compared to the national average.

Step-by-step explanation:

1. To find the probability that fewer than 2 out of 100 houses in the Washington, DC area will go up for foreclosure, we can use the binomial probability formula. Since the foreclosure rate is 1.31%, we want to find the probability of getting 0 or 1 foreclosures out of 100 houses. The formula is P(X ≤ 1) = 0.01C₀(1.31%)⁰(98.69%)¹ + 0.01C₁(1.31%)¹(98.69%)⁰.
2. To find the probability that fewer than 2 out of 100 houses in the nation will go up for foreclosure, we can use the same binomial probability formula. The foreclosure rate is 0.87%, so we want to find the probability of getting 0 or 1 foreclosures out of 100 houses. The formula is P(X ≤ 1) = 0.01C₀(0.87%)⁰(99.13%)¹ + 0.01C₁(0.87%)¹(99.13%)⁰.
3. The findings suggest that the foreclosure rate in the Washington, DC area is higher than the national average. This might indicate specific factors at play in the region, such as economic conditions or housing market dynamics. It could be an area of concern for policymakers and homeowners in the region.

Answer 2

a) 0.6226 = 62.26% probability that in a given year, fewer than 2 out of 100 houses in the Washington, DC area will go up for foreclosure.

b) 0.7837 = 78.37% probability that in a given year, fewer than 2 out of 100 houses in the nation will go up for foreclosure.

c) The proportion of foreclosures in the Nation is lower than in Washington, which means that with a sample size of 100, it is likely to have a small number(fewer than 2) of foreclosures than Washington DC.

Step-by-step explanation:

For each home, there are only two possible outcomes. Either it goes into foreclosure, or it does not. The probability of a home going into foreclosure is independent of other homes. This means that we use the binomial probability distribution to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

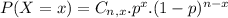
In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

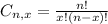
And p is the probability of X happening.

a. What is the probability that in a given year, fewer than 2 out of 100 houses in the Washington, DC area will go up for foreclosure?

The foreclosure rate is 1.31% for the Washington, DC area, which means that
`p = 0.0131`

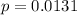
We wanto to find, with
`n = 100`:

`P(X < 2) = P(X = 0) + P(X = 1)`

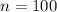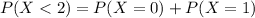
In which

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(100,0).(0.0131)^(0).(0.9869)^(100) = 0.2675`

`P(X = 1) = C_(100,1).(0.0131)^(1).(0.9869)^(99) = 0.3551`

`P(X < 2) = P(X = 0) + P(X = 1) = 0.2675 + 0.3551 = 0.6226`

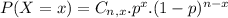
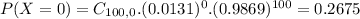
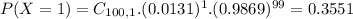
0.6226 = 62.26% probability that in a given year, fewer than 2 out of 100 houses in the Washington, DC area will go up for foreclosure.

b. What is the probability that in a given year, fewer than 2 out of 100 houses in the nation will go up for foreclosure?

Foreclosure rate of 0.87% for the nation, which means that
`p = 0.0087`. So

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(100,0).(0.0087)^(0).(0.9913)^(100) = 0.4174`

`P(X = 1) = C_(100,1).(0.0087)^(1).(0.9913)^(99) = 0.3663`

`P(X < 2) = P(X = 0) + P(X = 1) = 0.4174 + 0.3663 = 0.7837`

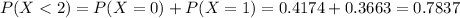
0.7837 = 78.37% probability that in a given year, fewer than 2 out of 100 houses in the nation will go up for foreclosure.

c. Comment on the above findings.

The proportion of foreclosures in the Nation is lower than in Washington, which means that with a sample size of 100, it is likely to have a small number(fewer than 2) of foreclosures than Washington DC.