Question

Suppose the gravitational force between two spheres is45 N. If the distance between the spheres is halved, whatis the force between the masses?

Answer 1

Given,

The gravitational force between two spheres, F=45 N

Let the initial distance between the spheres be r.

After the distance becomes half, the new distance between the spheres is,

`r_0=(r)/(2)`

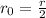
From Newton's universal law of gravitation, the gravitational force between two objects is proportional to the product of the mass of the objects and inversely proportional to the square of the distance between them.

Therefore, the initial gravitational force between the objects is,

`F=(GMm)/(r^2)\text{ }\rightarrow\text{ (i)}`

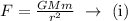
Where G is the gravitational constant, M and m are the mass of the spheres.

After the distance between the spheres becomes half, the gravitational force between th objects is,

`\begin{gathered} F_0=\frac{\text{GMm}}{r^2_0} \\ =(GMm)/(((r)/(2))^2) \\ =\frac{4\text{GMm}}{r^2_{}} \\ =4*(GMm)/(r^2)\text{ }\rightarrow\text{ (i}i) \end{gathered}`

From equation (i) and equation (ii),

`\begin{gathered} F_0=4* F \\ =4*45 \\ =180\text{ N} \end{gathered}`

Thus, when the distance between the spheres is halved, the force between them will increase to 180 N.