Answer:
0.6856
Explanation:
![\text{The missing part of the question states that we should Note: that N(108,20) model to } \\ \\ \text{ } \text{approximate the distribution of weekly complaints).]}](https://img.qammunity.org/qa-images/2022/formulas/mathematics/college/yzizmau5sqelattnz2u6sy.png)
Now; assuming X = no of complaints received in a week
Required:
To find P(77 < X < 120)
Using a Gaussian Normal Distribution (
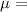 108,
108,
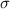 = 20)
= 20)
Using Z scores:
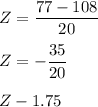
As a result X = 77 for N(108,20) is approximately equal to to Z = -1.75 for N(0,1)
SO;
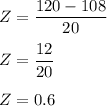
Here; X = 77 for a N(108,20) is same to Z = 0.6 for N(0,1)
Now, to determine:
P(-1.75 < Z < 0.6) = P(Z < 0.6) - P( Z < - 1.75)
From the standard normal Z-table:
P(-1.75 < Z < 0.6) = 0.7257 - 0.0401
P(-1.75 < Z < 0.6) = 0.6856