Answer:
1. Perimeter = 12 units
Area = 6 squared units
Step-by-step explanation:
The perimeter of the triangle is equal to the sum of the length of every side.
So, we know that the measures of the triangle are:
Now, to find x, we can apply the Pythagorean theorem, so:
![\begin{gathered} x^2=3^2+4^2 \\ x=\sqrt[]{3^2+4^2} \\ x=\sqrt[]{9+16} \\ x=\sqrt[]{25} \\ x=5 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/n31f90ivt310nm9miouiq0xc30vi6h0c7t.png)
Therefore, the perimeter of the triangle is:
Perimeter = x + 4 + 3 = 5 + 4 + 3 = 12
On the other hand, the area of the triangle can be calculated as:
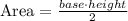
So, replacing the base by 4 and the height by 3, we get:
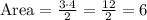
So, the perimeter of the 1st figure is 12 units and the area of the 1st figure is equal to 6 squared units.