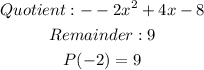Given;
There are given that the polynomial:

Step-by-step explanation:
To find the quotient and remainder, we need to find the value of P(-2):
Then,
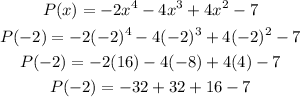
Then,
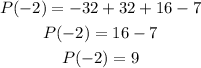
So, the remainder is 9.
Now,
For the quotient:
Divide the given polynomial by (x+2):
So,
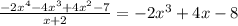
Final answer:
Hence, the quotient, remainder, and the value for P(-2) is shown below: