Given
Arithmetic sequence
100th term is 32 and the 200th term is 116.
Find
a) Difference ,d
b) First term , a
Step-by-step explanation
as we know that the nth term of an arithmrtic sequence is given by
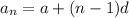
according to the question ,
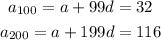
solve these two equation by elimination method .
subtract both equation to eliminate a ,
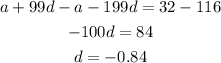
now put value of d in one of the equation,
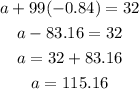
Final Answer
therfore , the difference = -0.84 and first term = 115.16