Question

An integer is 3 more than 4 times another. If the product of the two integers is 45, then findthe integers

Answer 1

Define the equations that describe the situation

`\begin{gathered} x=4y+3 \\ x\cdot y=45 \end{gathered}`

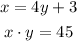
Clear x from the second equation

`x=(45)/(y)`

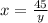
Make both equations equal

`\begin{gathered} 4y+3=(45)/(y) \\ y(4y+3)=45 \\ 4y^2+3y=45 \\ 4y^2+3y-45=0 \end{gathered}`

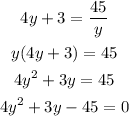
Solve the cuadratic equation

`\begin{gathered} y=\frac{-3\pm\sqrt[]{3^2-4\cdot4\cdot(-45)}}{2\cdot4} \\ y=\frac{-3\pm\sqrt[]{9+720}}{8} \\ y=(-3\pm27)/(8) \\ y1=-(30)/(8)=-(15)/(4) \\ y2=(24)/(8)=3 \end{gathered}`

As we are dealing with integers, the value of y is 3, now use one of the first equations to find x

`\begin{gathered} x=(45)/(y) \\ x=(45)/(3) \\ x=15 \end{gathered}`

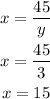
The integers are 3 and 15