Given the word problem, we can deduce the following information:
1. For the quarterly meeting this month, she reserved 4 conference rooms and 3 ballrooms, which can seat a total of 181 attendees.
2. For safety training next month, she reserved 2 conference rooms and 3 ballrooms, which can seat 155 attendees.
To determine the number of attendees can each room accommodate, we note first that the system of equations would be:

where:
c = attendees per conference room
b = attendees per ballroom
Now, we use elimination as shown below:
We subtract the 2nd row from the first row:
Next, we solve for c,
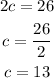
Then, we plug in c=13 into any of the two equations above:

Therefore, a conference room can accommodate 13 attendees, while a ballroom can accommodate 43 attendees.