Question

find the real solution(s), if any, of the system by examining the graph. verify the solutions algebraically

Answer 1

Step-by-step explanation

We are to analyze the system of equations graphically

For quadratic equations

If the graph of the quadratic function crosses the x-axis at two points then we have two solutions. If the graph touches the x-axis at one point then we have one solution. If the graph does not intersect with the x-axis then the equation has no real solution.

For the given simultaneous

`\begin{gathered} (x+1)^2+y^2=9 \\ y-3=-(1)/(3)(x+1)^2 \end{gathered}`

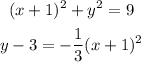
Plotting the two equations

From the graph, we have the solutions to be where the two graphs intersect

`\begin{pmatrix}x=-4.0000\: & y=0 \\ x=-1.0000\: & y=3 \\ x=2,\: & y=0\end{pmatrix}`

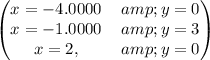
Therefore, there are 3 real solutions

Thus, the answer is