Question

In two or more complete sentences, describe the transformation(s) that take place on the parent function, f(x)=log(x), to achieve the graph of g(x)=log(−2x−4)−1.

Answer 1

We have the parent function:

`f(x)=\log (x)`

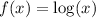
First, we are going to do a horizontal compression using the following rule:

`\begin{gathered} y=f(bx) \\ so\colon \\ f(x)=\log (2x) \end{gathered}`

Now, let's reflecte over y-axis:

`\begin{gathered} y=f(-x) \\ so\colon \\ y=\log (-2x) \end{gathered}`

Let's make a horizontal translation 4 units to the right:

`\begin{gathered} y=f(x-k) \\ f(x)=\log (-2x-4) \end{gathered}`

Finally, translate the function 1 unit down:

`\begin{gathered} y=f(x)-h \\ f(x)=g(x)=\log (-2x-4)-1 \end{gathered}`

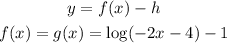
The red graph is f(x) anf the blue graph is g(x)