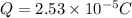Answer:
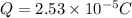
Step-by-step explanation: The amount of charge that moves into the capacitor plates depends upon the capacitance and the applied voltage, it is given by the following formula:
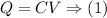
To find the charge on the capacitor we need to identify the knows and unknows as follows:
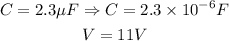
Plugging these values in formula (1) we get the answer as follows:
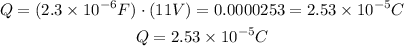
Therefore the charge on the capacitor is: