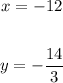Given:
The system of equations are
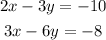
Required:
To solve the given system of equations using an inverse matrix.
Step-by-step explanation:
Write the system in terms of a coefficient matrix, a variable matrix, and a constant matrix.
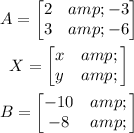
Then
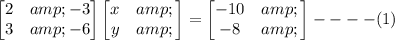
First, we need to calculate inverse of A. Using the formula to calculate the inverse of a 2 by 2 matrix, we have:
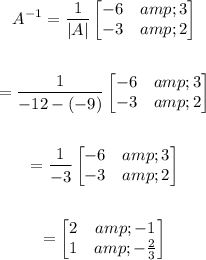
Now we are ready to solve. Multiply both sides of the equation by inverse of A,
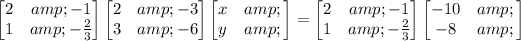
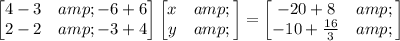
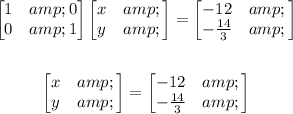
Final Answer:
The solution is