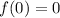Question

From the given information. Write the recursive and explicit functions for each arithmetic sequence. Use these terms please; recursive f(1) = first term, f(n) = pattern+f(n-1). Explicit: y = pattern*x + 0 term. work backwards to find 0 term

Answer 1

An arithmetic sequence has the form:

`f(n)=f(1)+d(n-1)`

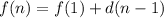
where d is the common difference.

For this sequence the common difference is 3 and the first term is:

`f(1)=3`

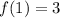
Plugging this values in the general expression we have:

`\begin{gathered} f(n)=3+3(n-1) \\ f(n)=3n-3+3 \\ f(n)=3n \end{gathered}`

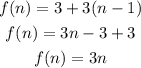
Therefore the sequence is:

`f(n)=3n`

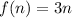
Now, from this expression we can determine the value of the zeroth term:

`\begin{gathered} f(0)=3(0) \\ f(0)=0 \end{gathered}`

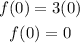
Hence the zeroth term is:

`f(0)=0`