Given:
the length of the cable is
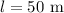
the mass of the cable is
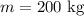
the tension force on the cable is
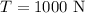
Required: velocity of the wave.
Step-by-step explanation:
to find the velocity of the wave on a cable we use the formula that is given by
![v=\sqrt[2]{(T)/(\mu)}](https://img.qammunity.org/2023/formulas/physics/college/5vb3h6eahwizlsgsqqpfxd7sdzqs4wy4k2.png)
Where
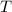
is the tension force and
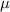
is mass per unit length.
first, we calculate the mass per unit length.
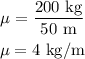
now put this value in the above relation and solve for velocity, we get
![\begin{gathered} v=\sqrt[2]{(T)/(\mu)} \\ v=\sqrt[2]{\frac{1000\text{ N}}{4\text{ kg/m}}} \\ v=15.81\text{ m/s} \end{gathered}](https://img.qammunity.org/2023/formulas/physics/college/tlg6y5ewdz4nv67kl1q6inm6l1bkc8rso8.png)
Thus, the speed of the wave is 15.81 m/s.