Solution
The slope of a straight line can be found from any graph by first drawing a triangle against the straight line indicating the rise and the run
The triangle usually is gotten by drawing straight lines from points on the graph where the line passes exactly across the intersection of lines of the y-axis and the x-axis
The circled points are good for usage to get the slope because the line passes exactly at the intersection of the vertical and horizontal line of the graph
Below is how the triangle will look
'The equation for the slope then is written as
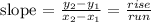
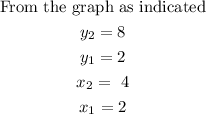
Therefore the slope after substitution is
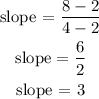
The slope = 3