Question:
Two sisters like to compete on their bike rides. Ciara can go 4 mph faster than her sister, Colleen. If it takes Colleen one hour longer than Ciara to go 80 miles, how fast can Colleen ride her bike?
Step-by-step explanation:
Note that Ciara can go 4mph faster than Collen.
Let's take the speed to ride a bike for Collen to be x mph.
The speed to ride a bike for Ciara will be (x + 4) mph
Now, to cover a distance of 80 miles, Collen takes 1 hour longer than Ciara. Applying the kinematics equation for motion at constant speed:
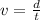
where v is velocity, d is distance and t is time, we can solve this equation for the time t:
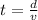
Here time Collen takes to cover a distance of 80 miles in 1 hour is more than that taken by Ciara, hence:
Time taken by Collen:
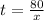
Time taken by Ciara:
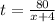
The equation for the difference in time:
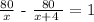
Solve the equation for the difference in time to get the value of x which is Collen speed:
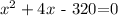
Solving the quadratic equation by the quadratic formula where a=1,b=4, and c=-320, we get:
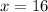
Answer: Colleen's speed is 16 mph.