We have to find the equation of the line, in point-slope form, that is perpendicular to y - 25 = 2(x - 10) and passes through (-3,7).
The line y - 25 = 2(x - 10) has a slope m = 2.
Perpendicular lines have slopes that are negative reciprocals, so our line will have a slope that is:

Then, we have the slope m = -1/2 and the point (-3,7), so we can write the point-slope form of the equation as:
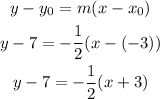
Answer: y - 7 = -1/2 * (x + 3) [Option C]