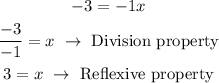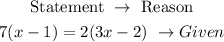
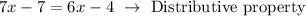
Beacuse to both sides of the equation you distribute the number that is outside the parentheses when making the product.
Then, you operate on both sides of the equation -7x, that is, you use the additive inverse of 7x
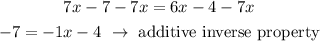
Then, you operate on both sides of the equation 4, that is, you use the add inverse of -4
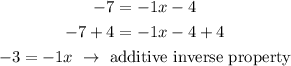
Finally,