Question

(1-9i)(1-4i)(4-3i)write the expression as a complex number and standard form

Answer 1

Since the brackets are

`(1-9i)(1-4i)(4-3i)`

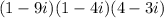
We will start to multiply the first 2 brackets, then multiply the answer by the 3rd bracket

`\begin{gathered} (1-9i)(1-4i) \\ 1st*1st=1*1=1 \end{gathered}`
`1st*2nd=1*(-4i)=-4i`
`2nd*1st=-9i*1=-9i`
`2nd*2nd=-9i*(-4i)=36i^2`

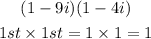
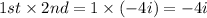
The value of i^2 is -1, then

`36i^2=-36`

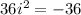
The answer to the product is

`(1-9i)(1-4i)=1-4i-9i-36`

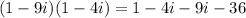
Add the like terms

`(1-9i)(1-4i)=(1-36)+(-4i-9i)=(-35-13i)`

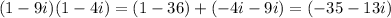
Now let us multiply the 3rd bracket by the answer

`\begin{gathered} (4-3i)(-35-13i) \\ 1st*1st=4*-35=-140 \end{gathered}`
`1st*2nd=4*(-13i)=-52i`
`2nd*1st=-3i*(-35)=105i`
`2nd*2nd=-3i*-13i=39i^2=-39`

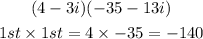
Now write them together and add the like terms

`\begin{gathered} -140+(-52i)+(105i)+(-39)= \\ (-140-39)+(-52i+105i)= \\ -179+53i \end{gathered}`

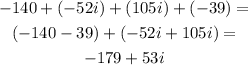
The product of the 3 brackets is -179 + 53i