Question

for certain workers, the mean wage is $7.00/hr. with a standard deviation of $0.25 . if a worker is chosen at random, what is the probability the worker's wage is between $6.50 and $7.50? assume a normal distribution of wages

Answer 1

The variable of interest is X: earnings of one worker.

This variable has a normal distribution with mean μ=$7.00/hr and standard deviation σ=$0.25

You need to determine the probability that a worker chosen at random earns between $6.50 and $7.50, symbolically:

`P(6.50\leq X\leq7.50)`

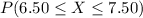
To determine the probability within these two values you have to subtract the accumulated probability until 6.50 to the accumulated probability until 7.50:

`P(6.50\leq X\leq7.50)=P(X\leq7.50)-P(X\leq6.50)`

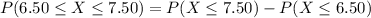
First, you have to determine the corresponding values of the variable under the standard normal distribution, i.e., you have to calculate the Z-values for 7.50 and 6.50:

`Z=(X-\mu)/(\sigma)N\sim(0,1)`
`P(X\leq7.50)=P(Z\leq(7.50-7)/(0.25))=P(Z\leq2)`
`P(X\leq6.50)=P(Z\leq(6.50-7)/(0.25))=P(Z\leq-2)`

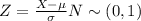
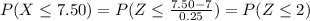
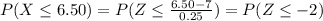
Next, you have to look for the accumulated probability under the standard normal distribution:

`P(Z\leq2)=0.977`

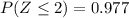
and

`P(Z\leq-2)=0.023`

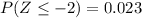
Now that you have determined the probabilities you can determine the asked one:

`\begin{gathered} P(6.5\leq X\leq7.5)=P(X\leq7.5)-P(X\leq6.5)= \\ P(Z\leq2)-P(Z\leq-2)=0.977-0.023=0.954 \end{gathered}`

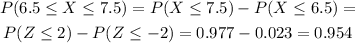
There is a 0.954 or 95.4% of probability that the worker choosen at random earns between $6.50/hour and $7.50/hour.