To solve the exercise, you can take the two points highlighted on the graph and use the slope formula
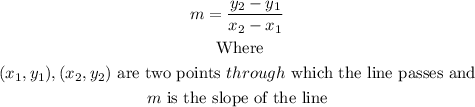
So, if you take
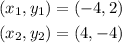
the slope of the line will be
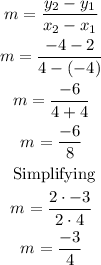
Now, with the point slope equation you can write the equation of the line in its slope-intercept form
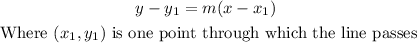
So, if you take the point (-4,2) you have
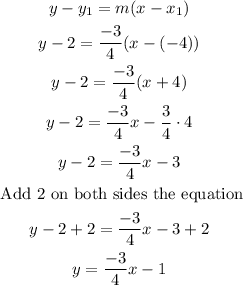
Then, the equation of the line in its slope-intercept form is
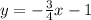
And to find out if the line passes through the origin, plug x = 0 into the equation found
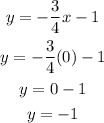
That means that the line passes through the point (0, -1) and not through the point (0,0). Therefore, the line does not pass through the origin, and the answer is False.
Finally, since the slope of the line is negative, then the line is decreasing.