Question

The perimeter of a rectangle is 84. The length is 2 1/2 times the width. Find the dimensions of the rectangle.

Answer 1

The Solution:

Given:

The perimeter of a rectangle is 84.

We are asked to find the dimensions ( that is, length and width) of the rectangle.

Let the length of the rectangle be L and W for the width.

So,

`L=2(1)/(2)of\text{ W}=(5)/(2)W`

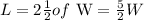
By formula, the perimeter of a rectangle is:

`\begin{gathered} P=2(L+W) \\ \\ In\text{ this case,} \\ P=perimeter=84 \\ W=width=? \\ L=length=(5)/(2)W \end{gathered}`

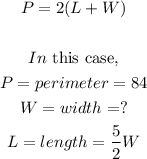
Substitute these values in the formula, we get:

`84=2((5)/(2)W+W)`

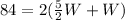
Dividing both sides by 2, we get:

`\begin{gathered} 42=(5)/(2)W+W \\ \\ 42=(5W+2W)/(2) \\ \\ 42=(7W)/(2) \end{gathered}`

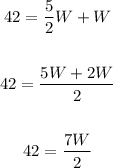
Cross multiplying, we get:

`\begin{gathered} 7W=2*42 \\ 7W=84 \end{gathered}`

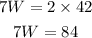
Dividing both sides by 7, we get:

`W=(84)/(7)=12`

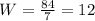
To find the length L, we shall put 12 for W.

`L=(5)/(2)W=(5)/(2)*12=5*6=30`

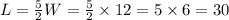
Therefore, the dimensions of the rectangle is 30 by 12.

Length = 30 units

Width = 12 units