Question

The velocity, in ft/sec of a particle is given by v(t) =-14t + 2. Find the position function s(t) of the particle if it has an initial position s(0) = 4 feet.

Answer 1

Option B is correct

`s(t)=-7t^(2)+2t+4`

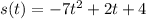
Explanations;

Given the velocity of the particle expressed as;

`v(t)=-14t+2`

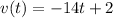
The position of the object is determined by integrating the velocity function as shown:

`\begin{gathered} s(t)=\int v(t)dt \\ s(t)=\int(-14t+2)dt \\ s(t)=-(14t^2)/(2)+2t_+C \\ s(t)=-7t^2+2t+C \end{gathered}`

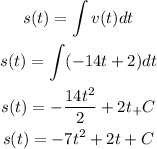
If the particle has an initial position s(0) = 4 feet, then;

`\begin{gathered} s(0)=-7(0)^2+2(0)+C \\ 4=C \end{gathered}`

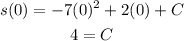
Substitute the constant into the position function to have:

`s(t)=-7t^2+2t+4`

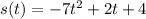
This gives the required position of the particle