GIVEN:
We are told that a motorcycle purchased for $20,200 depreciates at a constant rate of 15% per year.
Required;
Write the function that models the value of the motorcycle after t years.
What will the motorcycle be worth after 5 years?
Step-by-step solution;
For a value that depreciates at a given percentage, we use the exponential function. For an exponential decay (decrease in value), we use the following formula;
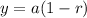
This represents the value as at the first year after purchase. Therefore, for the value after any number of years given the exponential part of the equation is raised to the power of the year in review.
Therefore, for t number of years, we now have;

For the value of the motorcycle after t number of years, we now have the following;
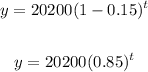
Therefore, for the value after 5 years we simply substitute t equals 5 in the equation.

We can now approximate this value and we'll have;
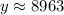
Therefore,
ANSWER;
The 4th option is the correct answer. The motorcycle will be worth $8,963 in the next 5 years.