Question

Please use the sum and difference formulas to simplify the following trigonometric expression.

Which expression is equivalent to
`\csc\alpha\csc\beta\cos(\alpha+\beta)` for all values of
`\alpha` and {tex}\beta{/tex} for which
`\csc\alpha\csc\beta\cos(\alpha+\beta)` is defined?

Answer 1

Answer: cot(a)cot(ß)-1

Explanation:

`\csc\alpha\csc\beta\cos(\alpha+\beta)=(\sin\alpha)^(-1)(\sin\beta)^(-1)\cos(\alpha+\beta)\\=(\sin\alpha\sin\beta)^(-1)\cos(\alpha+\beta)\\=(\cos\alpha\cos\beta-\sin\alpha\sin\beta)/(\sin\alpha\sin\beta)\\=(\cos\alpha\cos\beta)/(\sin\alpha\sin\beta)-1\\=\cot\alpha\cot\beta-1`

Answer 2

Hi there!

`\large\boxed{cot(a)cot(b)-1}`

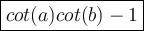
We can begin by simplifying cos(a + b) to find an equivalent expression.

With a sum of angles identity for cosine, we can determine that:

cos(a + b) = cos(a)cos(b) - sin(a)sin(b)

In this instance, we have to multiply this expression by csc(a)csc(b). Therefore:

(csc(a)csc(b)) · (cos(a)(cos(b) - sin(a)sin(b))

Distribute:

(csc(a)(csc(b))(cos(a)(cos(b)) - (csc(a)csc(b))(sin(a)sin(b))

Rewrite csc as 1/sin to simplify:

(1/sin(a) * 1/sin(b))(cos(a)(cos(b)) - (1/sin(a) * 1/sin(b))(sin(a)sin(b))

Multiply:

cos(a)/sin(a) * cos(b)/sin(b) - 1/sin(a) * sin(a) * 1/sin(b)*sin(b) <--- = 1

We now have remaining:

cos(a) / sin(a) * cos(b)/sin(b) - 1

Simplify to cotangent:

cot(a) * cot(b) - 1