Question

Consider the following functions. Find five ordered pairs that satisfy the sum of the functions, f(x)=x^2-5

Answer 1

(-2,8),(-1,2),(0,0)(1,2) and (2,8)

Step-by-step explanation:

Given the functions, f(x) and g(x) defined below:

`f(x)=x^2+5,g(x)=x^2-5`

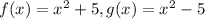
First, find the sum (say h(x)) of the functions f(x) and g(x):

`\begin{gathered} f(x)+g\mleft(x\mright)=x^2+5+x^2-5=2x^2 \\ \implies h(x)=2x^2 \end{gathered}`

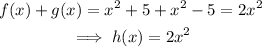
Next, we determine 5 ordered pairs for the sum:

`\begin{gathered} \text{When }x=-2,h(-2)=2(-2)^2=2*4=8\implies(-2,8) \\ \text{When }x=-1,h(-1)=2(-1)^2=2*1=2\implies(-1,2) \\ \text{When }x=0,h(0)=2(0)^2=2*0=0\implies(0,0) \\ \text{When }x=1,h(1)=2(1)^2=2*1=2\implies(1,2) \\ \text{When }x=2,h(2)=2(2)^2=2*4=8\implies(2,8) \end{gathered}`

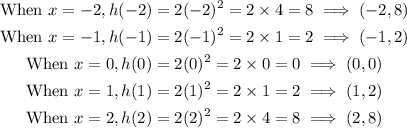
The 5 ordered pairs are (-2,8),(-1,2),(0,0)(1,2) and (2,8).