Solution
Step 1
Determine the number of shapes in figure 1
Figure 1 is made up of a cone and a hemisphere
Step 2
Write out the expression for the area of a cone and a hemisphere
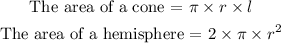
Where
pi =3.14
r = 7 inches
l = 15 inches
Step 3
Substitute in the values and find the area of the shape

Area = 637.42 square inches
Step 4
Determine the number of shapes in figure 2
Figure 2 is made up of a cone and a cylinder
Step 5
Write an expression for the area of a cylinder
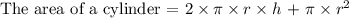
where h = 13yards
radius(r) = 11/2 = 5.5inches
l = ?
To find l, the slant height we use the Pythagoras theorem
so that
![\begin{gathered} l^2=11^2+9^2 \\ l^2=202 \\ l\text{ =}\sqrt[]{202} \\ l\text{ = 14.2126704 in} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/jy0rgqa0w0ka0fgwa6rgclnw9ey1jypxcd.png)
Step 6
Substitute in the values and find the area of the shape
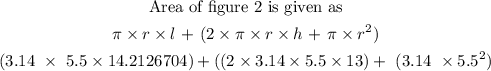

Area = 789.46 square inches