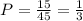Question

There are 6 forwards and 4 guards on the Tigers girls basketball team. Coach Briggs will randomly choose two captains for the next game. What is the probability that both captains will be forwards?

Answer 1

`(1)/(3)`

1) Let's find the sample space, i.e. the number of the total outcomes (favorable and not favorable). Let's consider that we need to pick 2 out of ten, that is our sample space.

`_(10)C_2=(10!)/(2!*8!)=45`

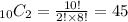
2) Now, let's find the number of favorable events. In this case, both players must be a forward. The favorable event includes only forward players out of those 6:

`_6C_2=(6!)/(2!(6-2)!)=15`

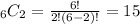
3) We can write out the probability of picking one forward and another forward. Note that there was no replacement after each picking:

`P=(15)/(45)=(1)/(3)`