Question

What can you say about the end behavior of the function ?A.f(x) is an even function so both ends of the graph go in opposite directions.B.The leading coefficient is negative so the left end of the graph goes up.C.The leading coefficient is negative so the left end of the graph goes down.D.f(x) is an even function so both ends of the graph go in the same direction.

Answer 1

C and D

Step-by-step explanation

We want to identify the options that are correct for the end behavior of the function:

`f(x)=-4x^6+6x^2-52`

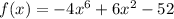
First, let us test to see if the function is even.

A function is even if:

`f(x)=f(-x)`

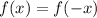
To find f(-x), substitute -x for x in the function:

`\begin{gathered} f(-x)=-4(-x)^6+6(-x)^2-52 \\ \\ f(-x)=-4x^6+6x^2-52 \end{gathered}`

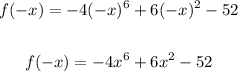
Since f(-x) is equal to f(x), we see that the function is even, hence, both ends of the graph go in the same direction.

The leading coefficient of a function is the coefficient of the term with the highest degree.

The leading coefficient of the given function is -4.

Since the leading coefficient is negative, it tends towards negative infinity as x increases, and so, the left end of the graph goes down.

Therefore, the options that are correct for the function are options C and D.