Question

Two bond funds pay interest at rates that differ by 4%. Money invested for one year in the first fund earns $600 interest. The same amount invested in the other fund earns $800. Find the lower rate of interest (in percent). %

Answer 1

Given:

The first fund earns $600 and the second fund earns $800.

Let x% be the lower rate of interest.

And x+4% be the higher rate of interest.

The difference between the amounts is,

`800-600=200`

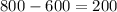
It means,

`\begin{gathered} 4\text{ percent of n =200} \\ \text{Where n is the amount invested. } \\ (4)/(100)* n=200 \\ n=(200*100)/(4) \\ n=5000 \\ It\text{ gives } \\ \text{x percent of }5000=600 \\ (x)/(100)*5000=600 \\ x=(600)/(50) \\ x=12 \\ \text{Same way,} \\ \text{x percent of }5000=800 \\ (x)/(100)*5000=800 \\ x=(800)/(50) \\ x=16 \end{gathered}`

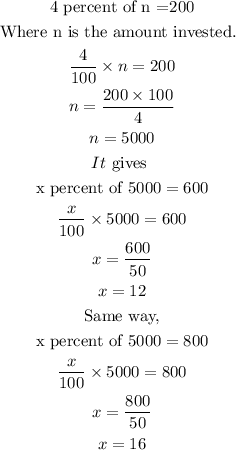
Alternative way,

For the first fund. let a be the lower rate and a+4 be the higher rate.

`ax=600`

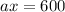
For second fund,

`\begin{gathered} x(a+4)=800 \\ ax+4x=800 \\ 600+4x=800 \\ 4x=800-600 \\ x=(200)/(4) \\ x=50 \end{gathered}`

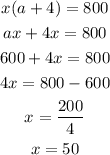
So,

`\begin{gathered} ax=600 \\ 50a=600 \\ a=(600)/(50) \\ a=12 \\ \Rightarrow a+4=12+4=16 \end{gathered}`

Answer: The lower rate of interest is 12%