Question

A golf ball of mass m = 0.12 kg is dropped from a height h. It interacts with the floor for t= 0.145 s, and applies a force of F= 18.5 N tothe floor when it elasticallycollides with it.Randomized Variablesm = 0.12 kgt=0.145 sF= 185 N b) what is the magnitude of the ball’s velocity v in meters per second, right after it rebounds? C) how high in meters will the ball travel on the rebound?

Answer 1

b)

We know that the impulse is related to the momentum as:

`I=\Delta p`

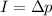
and to the force by:

`I=Ft`

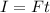
which means that:

`\begin{gathered} Ft=\Delta p \\ Ft=mv_f-mv_0 \\ Ft=m(v_f-v_0) \end{gathered}`

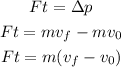
But we know that the collision is elastic which means that the velocity after the colision has the same magnitude than before the collison but with opposite sign, hence:

`\begin{gathered} Ft=2mv \\ v=(Ft)/(2m) \end{gathered}`

Plugging the values given we have that:

`\begin{gathered} v=((18.5)(0.145))/(2(0.12)) \\ v=11.177 \end{gathered}`

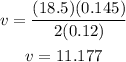
Therefore, the velocity right after the rebound is 11.177 m/s

c)

To determine how high in meters the ball will travel after the rebound we need to remember that the force acting on the ball is that of its weight which means that its acceleration is the acceleration of gravity and hence, the motion is an uniformly accelerated motion. Since we know the initial velocity, the acceleration and the final velocity (which will be zero at the highest point) we can use:

`v_f^2-v_0^2=2ay`

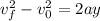
To find the height; plugging the values we have that:

`\begin{gathered} 0^2-11.177^2=2(-9.8)y \\ y=(-11.177^2)/((2)(-9.8)) \\ y=6.374 \end{gathered}`

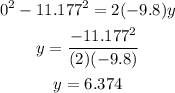
Therefore, the ball will reach a height of 6.374 m