To answer this question we will use the following formula for monthly compounded interest:
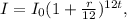
where I₀ is the initial amount, r is the interest rate as a decimal number, and t is the number of years.
Substituting I₀=2000, r=0.08, and t=15 we get:
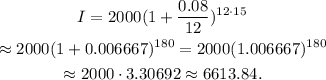
Answer: $6613.84.