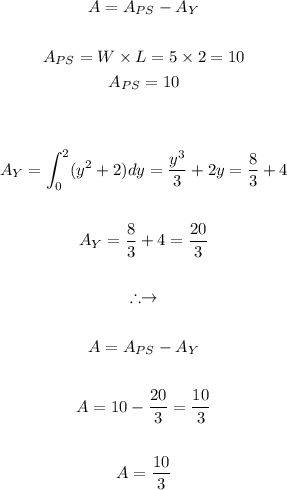Answer:
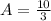
Step-by-step explanation: We have to find the area enclosed, which basically means the area in between the two:
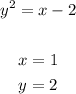
The plot of the above is as follows:
We have to find the purple shaded area in the above figure. this area would be equal to the area of the rectangle associated with the purple region minus the yellow shaded area:
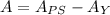
The Mathematical solution steps are as follows: