Step-by-step explanation
We must plot the function:

With values -10 ≤ x ≤ 10 and -10 ≤ y ≤ 10.
Taking into account the properties of logarithms:
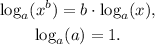
We evaluate the function at x = 1/2, 1, 2, 4 and 8:
![\begin{gathered} f((1)/(2))=\log_{(1)/(2)}((1)/(2))=1, \\ f(1)=\log_{(1)/(2)}(1)=0, \\ f(2)=\operatorname{\log}_{(1)/(2)}(2)=\operatorname{\log}_{(1)/(2)}(((1)/(2))^(-1))=-1\cdot\operatorname{\log}_{(1)/(2)}((1)/(2))=-1, \\ f(4)=\operatorname{\log}_{(1)/(2)}(4)=\operatorname{\log}_{(1)/(2)}(((1)/(2))^(-2))=-2\cdot\operatorname{\log}_{(1)/(2)}((1)/(2))=-2, \\ f(8)=\operatorname{\log}_{(1)/(2)}(8)=\operatorname{\log}_{(1)/(2)}(((1)/(2))^(-3))=-3\cdot\operatorname{\log}_{(1)/(2)}((1)/(2))=-3. \end{gathered}]()
Plotting these values and the function, we get the following graph:
Answer
Points:
• (1/2, 1)
,
• (1, 0)
,
• (2, -1)
,
• (4, -2)
,
• (8, -3)
Graph: