Question

A professor went to a website for rating professors and looked up the quality rating and also the "easiness" of the six full-time professors in onedepartment. The ratings are 1 (lowest quality) to 5 (highest quality) and 1 (hardest) to 5 (easiest). The numbers given are averages for eachprofessor. Assume the trend is linear, find the correlation, and comment on what it means.

Answer 1

We are asked to determine the correlation factor "r" of the given table. To do that we will first label the column for "Quality" as "x" and the column for "Easiness" as "y". Like this:

Now, we create another column with the product of "x" and "y". Like this:

Now, we will add another column with the squares of the values of "x". Like this:

Now, we add another column with the squares of the values of "y":

Now, we sum the values on each of the columns:

Now, to get the correlation factor we use the following formula:

`r=(n\Sigma xy-\Sigma x\Sigma y)/(√((n\Sigma x^2-(\Sigma x)^2)(n\Sigma y^2-(\Sigma y)^2)))`

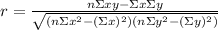
Where:

`\begin{gathered} \Sigma xy=\text{ sum of the column of xy} \\ \Sigma x=\text{ sum of the column x} \\ \Sigma y=\text{ sum of the column y} \\ \Sigma x^2=\text{ sum of the column x\textasciicircum2} \\ \Sigma y^2=\text{ sum of the column y\textasciicircum2} \\ n=\text{ number of rows} \end{gathered}`

Now we substitute the values, we get:

`r=(\left(6)(70.56)-(25.2)(16.4\right))/(√(((6)(107.12)-(25.2)^2)((6)(47.82)-(16.4)^2)))`

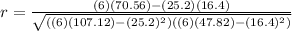
Solving the operations:

`r=0.858`

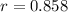
Therefore, the correlation factor is 0.858. If the correlation factor approaches the values of +1, this means that there is a strong linear correlation between the variables "x" and "y" and this correlation tends to be with a positive slope.