The formula to find the area of a circle is
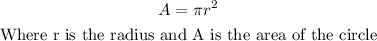
So as you can see, if you have the area of the circle, you can see get the measure of its radius:
![\begin{gathered} A=289\pi m^2 \\ A=\pi r^2 \\ 289\pi m^2=\pi r^2 \\ \text{ Divide by }\pi\text{ from both sides of the equation} \\ (289\pi m^2)/(\pi)=(\pi r^2)/(\pi) \\ 289m^2=r^2 \\ \text{ Apply square root to both sides of the equation} \\ \sqrt[]{289m^2}=\sqrt[]{r^2} \\ 17m=r \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/sqldtdcbs4ekax7zcpw4q81d8nbeyg28ej.png)
Now that you have the measure of the radius of the circle, you can obtain its circumference using this formula:
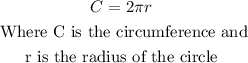
So, you have
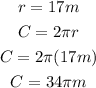
Therefore, the correct answer is option B.