From the problem, we have :
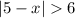
In solving absolute values, we need to take the positive and negative values of the terms outside the absolute value sign.
This will be :
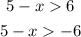
We will form two inequalities.
Solve for the solutions :
For the first inequality,
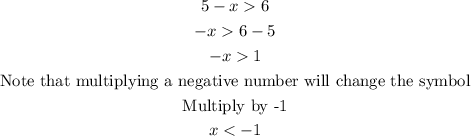
For the second inequality,
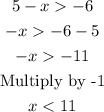
So we have x < -1 and x < 11
From these two solutions, x < -1 will govern since that inequality needs a value of x less than -1 and some of the numbers less than 11 will not apply to it.
So the answer is x < -1
The graph will be :
The end point is an open circle because the symbol is <